

.jpg)






.jpg)



.jpg)







.jpg)



.jpg)






.jpg)

驚人的數學魔術:18堂課,輕鬆變身數學A咖
相關專欄
書活網特推
◆本書初版誤植部分,再版已經更正。讀者請點此下載勘誤,以便確認正確解答。造成您的不便,敬請見諒。
內容簡介
臺師大特殊教育中心、國科會「第一屆中學科學資優教學設計競賽」金牌奬教師的創意學習法,
讓你輕鬆搞懂數學概念!
從魔術的玩法中,發現數學的趣味,
學會變魔術的同時,你也能成為驚人的數學A咖!
◎完全對應考題!
概念之後附有相對應的「基測」及「會考」試題,拿高分不是夢!
◎更完整、更好懂!
架構明確,從魔術提升學習興趣,再利用簡單的設問,引導貼近核心數學概念。
沒有不喜歡數學的人,只是還沒找到有趣的學習方法!
你絕對沒想過,利用撲克牌、骰子、錢幣等唾手可得的生活小物,也可以學習質因數分解、奇偶數、一次函數,甚至是最令人頭痛的幾何圖形與方程式!就連讀心術與預測未來的神奇魔法,也藏有數學的規律性!利用魔術翻轉數學,學習更具娛樂性與挑戰性!
此外,食衣住行育樂也都藏有數學的奧秘。與其硬背數學概念與公式,不如以充滿變化的魔術,突顯數學生活化的一面,並從中思考數學原理,充分吸收後再加以應用。
書中並附詳盡的數學學習單與基測、會考試題,帶你挑戰18堂數學魔術課的同時,扎實增進數學能力!
◆各界推薦
就是數學魔術的魔法,讓一個一個中輟生回來上課了,尤其熱切等待的就是數學課。教得不起勁的老師,主動追隨教師工作坊學習,再也不提退休了。-- 臺灣師範大學講座教授 林福來
數學魔術的「有趣」與課程的「有用」訴求互補,豐富教師與學生的數學學習經驗。-- 臺灣師範大學數學系退休教授 洪萬生
這些老師都太棒了,如果沒機會上他們的課,就趕快來看他們精彩的書,從魔術變出魔數!--中研院數學所兼任研究員李國偉
這本書提供了「為什麼學數學?」的良好解答,真是一本數學教育界工作者值得閱讀的書。--臺灣師範大學數學系教授 謝豐瑞
能促進親子與師生關係,又能獲得數學知識的難得好書!--彰化師範大學數學系教授 施皓耀
書中介紹的魔術流程很容易,但效果非常好,希望讀者能體會其中的數學奧妙。-- 國立師範大學數學系教授 郭君逸
見證數學邏輯幻化成奧妙魔術時的學習奇蹟!-- 長庚大學電子工程系助理教授 賴以威
數學經魔術烘焙,絲毫沒有複雜程序和公式感。-- 國立東華大學應用數學系副教授 魏澤人
有效結合數學原理與魔術效果,誘發學習興趣。-- 淡江大學航空太空工程學系副教授 蕭富元
接下來,是見證數學奇蹟的時刻!-- 國際魔術大師 劉謙
作者簡介
吳如皓
十年前在課堂上做了一個「很平凡」的猜生日數字魔術後,因為學生有了「原來學數學這麼有意義」的反應與回饋,進而發現數學魔術可以用奇特的現象啟動學生的好奇心,然後引發觀察、記錄、操作、推論等一系列的思維活動去慢慢靠近答案。原來,魔術的奧祕,就是數學的奧秘!而十年來,對數學魔術的研究讓自己看到更多學習數學的可能,以及更多學生的想法與創意。魔術讓數學更貼近學生的世界,也讓自己在教學的路上更充滿熱情。
林壽福
致力推廣數學教育,並投入偏鄉進行數學魔術與數學奠基模組交流,深獲師生喜愛。因發現大家都在精彩的「魔力」薰習下,對學習數學產生了非常強的動力。因此希望透過生活化的趣味數學步道與數學魔術,啟動學生學習動力,獲得成就感,建立學習信心。感受到學習數學的有趣、有用,並且驚訝數學竟能使魔術更有威力!非常贊同與呼應愛因斯坦的主張「教師的主要任務,是喚醒學生對創造與知識的樂趣。」今年榮獲臺灣師範大學傑出校友。
莊惟棟
十二歲那年第一次發明數學魔術,第一位觀眾就是我的「數學老師」,那次老師的鼓勵給我持續的動力。當自己也成為老師後,覺得老師就像廚師,煮出色香味俱全的料理才能引人入勝。因此致力於豐富數學具像化的色彩,開啟學生品嚐數學的動機。數學的困難點恰好是魔術的迷人點,而其中,魔術是矛盾基本認知的藝術,數學是找到科學邏輯的技術,而數學技術恰可成就魔術藝術!實踐後讓學生在欣喜探究與熱烈討論之餘,學習數學的香、增進知識的味!

得獎紀錄
媒體「國中大會考專刊」推薦
博客來自然科學類No.3
規格
ISBN:9789861364575
304頁,17X23cm,西翻,平裝,套色(彩色頁32頁)
目錄
第一變 連環計 (學習:常數函數及一次函數)
第二變 混水摸幣 (學習:奇偶數、因數、倍數)
第三變 虛張聲勢 (學習:不等式)
第四變 瞞天過海 (學習:幾何圖形)
第五變 九為上策 (學習:因數、倍數、餘數、倍數判別法)
第六變 餘中生有 (學習:因數、倍數、餘數)
第七變 關門偷心 (學習:質因數分解)
第八變 圍魏救趙 (學習:推理與證明)
第九變 擒賊擒王 (學習:函數與對應)
第十變 以逸待勞 (學習:公因數、公倍數、最大公因數與最小公倍數、互質)
第十一變 借詩還原 (學習:等差數列)
第十二變 欲擒故縱 (學習:變量與不變量)
第十三變 順手牽數 (學習:一元一次、二元一次)
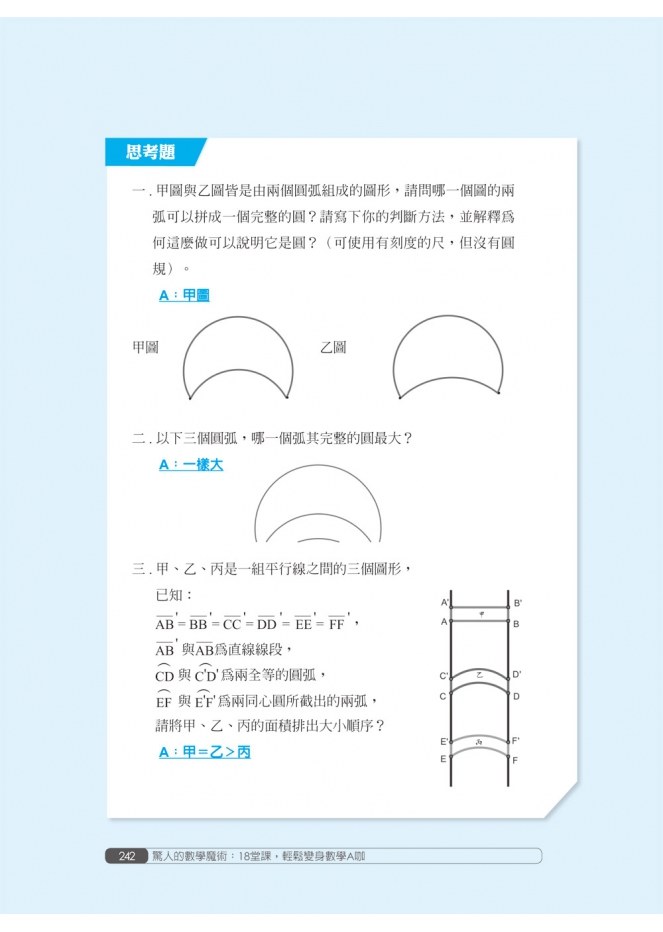
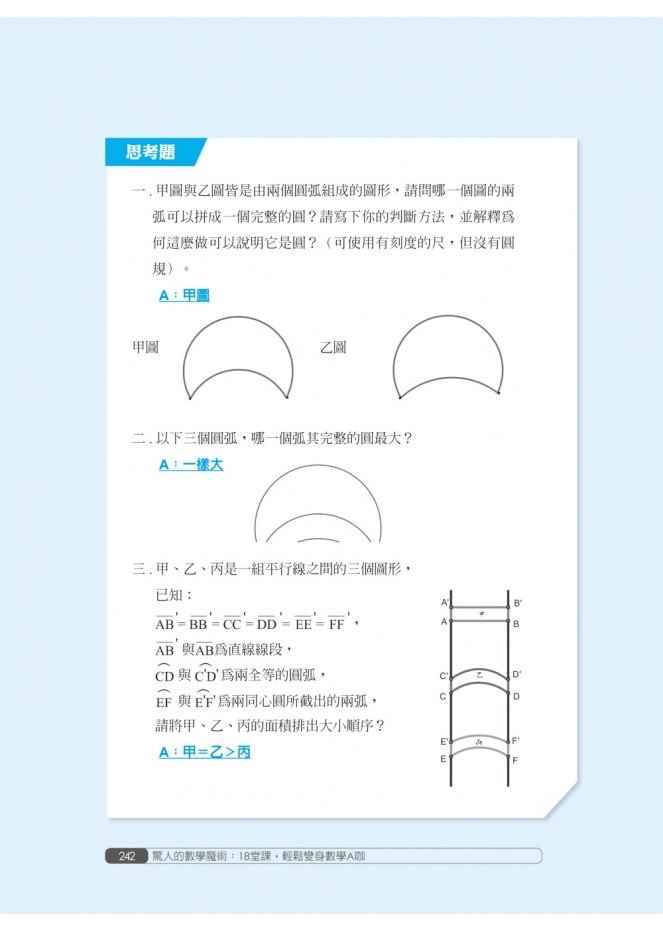
第十四變 反長為短 (學習:圓弧的性質)
第十五變 美人計 (學習:符號算式)
第十六變 反轉計 (學習:質因數的分解、二次方根)
第十七變 打草驚蛇 (學習:代數運算)
第十八變 暗渡陳倉 (學習:等差級數、由已知推未知)
序
自序
這本書的書名是《驚人的數學魔術》,它想談論的對象是魔術還是數學呢?講述的是數學的巧妙應用?還是在分解動作中逐步探究魔術的奧秘?是把數學扮成魔術?抑或是努力從魔術中看到數學的身影?
對筆者來說,這本書裡有聲音、有流動的光,把抽象概念組合成某種畫面,那畫面在心中留下深刻印象,然後把想像和思考匯聚成追蹤線索的腳力,開始闖蕩。筆者便在闖蕩的過程中啟發自己。
這本書真正想投入的領域是「數學教學」,數學是目標,魔術是手段。然而,不論透過哪一種教學手段,不同的學生所感受到的數學世界就大不相同。筆者曾經查過維基百科上對「數學」的簡介:「數學是利用符號語言,研究數量、結構、變化以及空間模型等概念的一門學科。」然後筆者又去查搞怪的偽基百科上對「數學」的簡介,卻是:
數學 = 一種很奇怪的科目。
一些數學家不停地想一些未有人能解答的問題 OR 與現實無關的問題
→ 另有一些數學家耗盡精力去解答問題。
那麼,現在學生心中的數學有什麼樣的長相呢?教學者在數學教學的過程中又讓學生建立了什麼樣的經驗、觸發了什麼樣的認識呢?筆者想說「學習數學是一種微妙的心理狀態」,每一個人學習過程中的解讀、吸收、思考都衍生那麼多的不同,然而,教學者是否能從更多元的面向讓學生感受數學是什麼、數學在做什麼呢?
如果有機會從更大的視野來看數學教學的意義,談論以數學魔術融入教學時,就不會只能從精采有趣來建立它的價值,數學魔術是學生進入數學世界的奇特切入點,是新的感覺,更是新的思考與突破。
然而,「魔術」在教學中到底扮演什麼樣的角色呢?「魔術」有一種趣味的定義:「魔術是一項務求違反客觀現象的表演藝術。」首先,魔術強化了數學抽象概念的情感成份,並且在巧妙地違反客觀現象的同時,製造了認知上的衝突,這種視覺與思考的撞擊使接下的探索與嘗試更有感覺。而有感覺的摸索過程,就是學生對數學方法最直接的體驗。學生心中對數學的感知不該只是一堆零亂的小碎片,本書的十八個數學魔術,不僅是為了得到數學知識,而是為了讓學生體驗數學思考的方法。這讓筆者想到洪萬生教授說的一句話:「數學很棒啊,它教會你不要困惑於事情的表象,有些簡單的答案就藏在那裡——而你用對了工具,就能發現。」魔術很棒,它會讓你暫時困惑於事情的表象,明明知道有個簡單的答案藏在裡頭,卻看不到,得懷抱著好奇與熱情,去追索混亂表象背後永恆不變的規律。
對於數學魔術持續的研究,一直提供筆者源源不絕的創造力與新想法。人為的藝術包裝數學,這樣的概念讓數學產生了不一樣的相貌。「到底為什麼會這樣?」的懷疑與好奇心,為主動思維提供了情意上的動機。本書從撲克牌、小紙片、硬幣、計算機的操作中展開十八個數學魔術,在不可能中製造機會、在機會中看到永恆的確立,從這裡開始體驗潛藏在魔術背後的數學風光。
本書能夠順利出版,要感謝許多貴人相助。親炙林福來教授6年,老師在數學教育的創見與開闊視野,豐盈我們教與學經驗;在臆測與概念奠基活動設計工作坊,親自指導我們探究數學活動的概念根源與知識結構,以及如何經營好的數學經驗。施皓耀教授利用生根計畫不斷幫我們專業增能,協助我們更貼近數學的本質,指導我們如何和學生談論現象與發展概念的核心。洪萬生教授指導我們學習數學的多元面向,培養我們的文化格局與人文品味。謝豐瑞教授指導我的解析數學語言,用更細膩的眼光看待教與學問題。另外,特別感謝廖惠儀老師,在形成這本書的過程中不斷參與討論,在數學引用、魔術敘述、學習單設計、書稿校閱等方面都給我們極好的意見,讓我們在寫書的過程有更豐富的想法,以及體驗切磋琢磨的快樂。
最後感謝所有教授,在此特別感謝知名魔術大師的推薦與指導。





.jpg)








.jpg)



